CFCC(Carbon Fiber Composite Cable)

General Information of CFCC

Characteristics of CFCC

General Information of CFCC

Outline of CFCC

Making the most of carbon fiber's excellent material properties, CFCC shows superior performances in terms of High Tensile Strength, Flexibility, Lightweight, High Corrosion Resistance, Non-Magnetism, and Low Linear Expansion in comparison with conventional cables. CFCC can be easily winded into a coil or onto a reel because of its stranded construction, thus can be applied as long span cables.

Notes on handling CFCC:
CFCC is a composite material consisting of carbon fibers and a matrix resin. As CFCC is different from steel members, special care should be taken; i.e. not to cause flaws, deformation or deterioration on handling. Especially, refrain from dropping hard and heavy objects (such as hammers) / sparking of welding/fire on CFCC, or bending CFCC steeply. CFCC damaged by any of these should be discarded.

Standard Specifications

Terminal Fixers

Formed Parts

Standard Characteristics

Standard Specifications

Standard specifications of CFCC are shown below:

Tendons: CFCC

(Cross section figure)	Designation	Diameter (mm)	Effective cross-sectional area (mm²)	Guaranteed breaking load (kN)	Unit weight per meter (g/m)	Elastic modulus (kN/mm²)
Uni-strand	U 5.0Φ	5.0	15.9	40.4	30	165
7 strands	1×7 7.9Φ	7.9	31.1	79.3	60	150
	1×7 10.8Φ	10.8	57.8	147.2	112	150
	1×7 12.5Φ	12.5	75.6	192.5	146	150
	1×7 15.2Φ	15.2	115.6	294.4	223	150
	1×7 17.2Φ	17.2	151.1	385.0	292	150
	1×7 19.3Φ	19.3	186.7	475.6	360	150
	1×7 26.2Φ	26.2	339.2	864.1	655	150
	1×7 28.9Φ	28.9	412.5	1,051	796	150
19 strands	1×19 34.3Φ	34.3	567.0	1,342	1,095	145
37 strands	1×37 40.9Φ	40.9	798.7	1,765	1,544	145

(Cross section figure)	Uni-strand
Designation	U 5.0Φ
Diameter (mm)	5.0
Effective cross-sectional area(mm²)	15.9
Guaranteed breaking load(kN)	40.4
Unit weight per meter(g/m)	30
Elastic modulus(kN/mm²)	165
(Cross section figure)	7 strands
Designation	1×7 7.9Φ
Diameter (mm)	7.9
Effective cross-sectional area(mm²)	31.1
Guaranteed breaking load(kN)	79.3
Unit weight per meter(g/m)	60
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 10.8Φ
Diameter (mm)	10.8
Effective cross-sectional area(mm²)	57.8
Guaranteed breaking load(kN)	147.2
Unit weight per meter(g/m)	112
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 12.5Φ
Diameter (mm)	12.5
Effective cross-sectional area(mm²)	75.6
Guaranteed breaking load(kN)	192.5
Unit weight per meter(g/m)	146
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 15.2Φ
Diameter (mm)	15.2
Effective cross-sectional area(mm²)	115.6
Guaranteed breaking load(kN)	294.4
Unit weight per meter(g/m)	223
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 17.2Φ
Diameter (mm)	17.2
Effective cross-sectional area(mm²)	151.1
Guaranteed breaking load(kN)	385.0
Unit weight per meter(g/m)	292
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 19.3Φ
Diameter (mm)	19.3
Effective cross-sectional area(mm²)	186.7
Guaranteed breaking load(kN)	475.6
Unit weight per meter(g/m)	360
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×19 26.2Φ
Diameter (mm)	26.2
Effective cross-sectional area(mm²)	339.2
Guaranteed breaking load(kN)	864.1
Unit weight per meter(g/m)	655
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×19 28.9Φ
Diameter (mm)	28.9
Effective cross-sectional area(mm²)	412.5
Guaranteed breaking load(kN)	1,051.0
Unit weight per meter(g/m)	796
Elastic modulus(kN/mm²)	150
(Cross section figure)	19 strands
Designation	1×19 34.3Φ
Diameter (mm)	34.3
Effective cross-sectional area(mm²)	567.0
Guaranteed breaking load(kN)	1,342.0
Unit weight per meter(g/m)	1,095
Elastic modulus(kN/mm²)	145
(Cross section figure)	37 strands
Designation	1×37 40.9Φ
Diameter (mm)	40.9
Effective cross-sectional area(mm²)	798.7
Guaranteed breaking load(kN)	1,765.0
Unit weight per meter(g/m)	1,544
Elastic modulus(kN/mm²)	145

Reinforcements: CFCC - RC

(Cross section figure)	Designation	Diameter (mm)	Effective cross-sectional area (mm²)	Guaranteed breaking load (kN)	Unit weight per meter (g/m)	Elastic modulus (kN/mm²)
Uni-strand	U 5.3Φ	5.3	17.9	31.7	34	160
	U 7.2Φ	7.2	32.7	58.1	62	160
	U 9.7Φ	9.7	59.5	105.6	112	160
7 strands	1×7 13.0Φ	13.0	83.3	147.8	159	150
	1×7 15.9Φ	15.9	125.0	221.7	238	150
	1×7 18.4Φ	18.4	166.7	295.6	317	150
	1×7 19.5Φ	19.5	187.5	332.6	357	150
	1×7 26.8Φ	26.8	354.2	628.2	675	150
	1×7 29.1Φ	29.1	416.7	739.1	794	150

(Cross section figure)	Uni-strand
Designation	U 5.3Φ
Diameter (mm)	5.3
Effective cross-sectional area(mm²)	17.9
Guaranteed breaking load(kN)	31.7
Unit weight per meter(g/m)	34
Elastic modulus(kN/mm²)	160
(Cross section figure)	Uni-strand
Designation	1×7 7.2Φ
Diameter (mm)	7.2
Effective cross-sectional area(mm²)	32.7
Guaranteed breaking load(kN)	58.1
Unit weight per meter(g/m)	62
Elastic modulus(kN/mm²)	160
(Cross section figure)	Uni-strand
Designation	1×7 9.7Φ
Diameter (mm)	9.7
Effective cross-sectional area(mm²)	59.5
Guaranteed breaking load(kN)	105.6
Unit weight per meter(g/m)	112
Elastic modulus(kN/mm²)	160
(Cross section figure)	7 strands
Designation	1×7 13.0Φ
Diameter (mm)	13.0
Effective cross-sectional area(mm²)	83.3
Guaranteed breaking load(kN)	147.8
Unit weight per meter(g/m)	159
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 15.9Φ
Diameter (mm)	15.9
Effective cross-sectional area(mm²)	125.0
Guaranteed breaking load(kN)	221.7
Unit weight per meter(g/m)	238
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 18.4Φ
Diameter (mm)	18.4
Effective cross-sectional area(mm²)	166.7
Guaranteed breaking load(kN)	295.6
Unit weight per meter(g/m)	317
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×7 19.5Φ
Diameter (mm)	19.5
Effective cross-sectional area(mm²)	187.5
Guaranteed breaking load(kN)	332.6
Unit weight per meter(g/m)	357
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×19 26.8Φ
Diameter (mm)	26.8
Effective cross-sectional area(mm²)	354.2
Guaranteed breaking load(kN)	628.2
Unit weight per meter(g/m)	675
Elastic modulus(kN/mm²)	150
(Cross section figure)	7 strands
Designation	1×19 29.1Φ
Diameter (mm)	29.1
Effective cross-sectional area(mm²)	416.7
Guaranteed breaking load(kN)	739.1
Unit weight per meter(g/m)	794
Elastic modulus(kN/mm²)	150

*Values in this table are standard values and are subject to change without prior notice.

Structural Symbols and Cross Section of CFCC

CFCC Structures	Structural symbol	Cross-section figure
Uni-strand	U
7 strands	1x7
19 strands	1x19
37 strands	1x37

Terminal Fixers

Terminal fixing methods currently applied for CFCC are roughly distinguished into 3 types shown below:

Resin filling method	Type	Symbol
Expansive material filling method	For single cable (CFCC 1 pc.)	ES
Expansive material filling method	For multiple cables (CFCC more than 2 pcs.)	EM
Wedge with buffer material method	For single cable (CFCC 1 pc.)	WS

1. Assembly of CFCC and terminal fixers is to be done at Tokyo Rope factory.
2. Terminal fixing methods other than above-mentioned are under development to meet diversified usages.

Formed Parts

CFCC can be formed into various shapes at our factory.
These parts can be used as reinforcing members for concrete structures.

Standard characteristics

Property	Item	Characteristic value Character istic value
General mechanical property	Tensile strength kN/mm² *1	CFCC	CFCC-RC
		2.55	1.77
	Tensile modulus kN/mm² *1	150
	Breaking elongation (%)	1.7
	Gravity	1.6
Static property	Ratio of relaxation (%) *2	1.3
	Creep strain *3	0.07x10^-3
	Coefficient of linear expansion (x10^-6 /°C) *4	0.6
	Specific resistance (µΩcm)	3,000
	Creep failure load ratio *5	0.85
Miscellaneous	Fatigue capacity (N/mm²) *6	780
	Bending stiffness kN·cm²	56.9
	Heat resistance (°C)	130～180
	Acid resistance	Superior to steel
	Alkali resistance	Equal to steel

※1. The value was calculated with effective cross-sectional area. (7 strands)
※2. 0.7pu, 1000hrs (20±2°C), in conformity with JSCE-E534
※3. 0.6pu, 1000hrs (20±2°C)
※4. 20°C-200°C, in conformity with JSCE-E536
※5. Creep failure load ratio measured at 1,000,000hrs, according to JSCE-E533 "Test method for creep failure of continuous fibers"
※6. Average stress is 75% of guaranteed breaking load, 2x106 cycles, according to JSCEE-535.

pu:The guaranteed breaking load

CFCC Grid

English (PDF:223KB) / Japanese (PDF:825KB)

Characteristics of CFCC

Characteristics of CFCC - 1

Unique, Outstanding Capabilities of CFCC that surpass conventional cables

"CFCC" stands for Carbon Fiber Composite Cable.
CFCC is a stranded CFRP (Carbon Fiber Reinforced Polymer) which consists of twisted carbon fibers of approx. 7µm dia. and an epoxy resin.

Characteristics of CFCC - 2

CFCC makes the most of carbon fiber's excellent material properties, and shows the merits superior to conventional cables.

Lightweight

About 1/5 weight of steel strands, with specific gravity of 1.5

15m→2.3kg (CFCC 1x7 12.5Φ)

Flexibility

Thanks to the stranded configuration, CFCC can be easily winded into a coil or on a reel.

CFCC 1x7 12.5mm diameter 1,200m long, winded onto a wood reel (shell diameter: 1.2m).

High Corrosion Resistance

CFCC has superior resistance to acid and alkali.

Non-Magnetism

CFCC is made from carbon fibers and an epoxy resin, thus is not magnetized.

Magnetic permeability

Material	Relative magnetic permeability
CFCC	Below 1.000*
Non magnetic PC steel (18Mn steel)	1.003
Iron core	1,200

* Due to the performance of magnetic analysis equipment, values less than 1.000 were immeasurable.

Low Linear Expansion

CFCC's coefficient of linear expansion is approx. 1/20 of steel.

Coefficient of linear expansion

Material	Coefficient of linear expansion
CFCC	0.6x10^-6/°C
Steel	12.0x10^-6/°C

High Tensile Strength

Tensile strength of CFCC is 1.4 - 2.1kN/mm².

High Tensile Elasticity

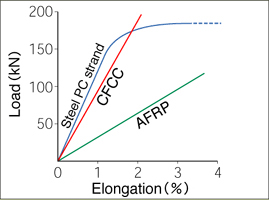
CFCC's tensile elastic modulus of 137kN/mm² is higher than glass fibers or aramid fibers.

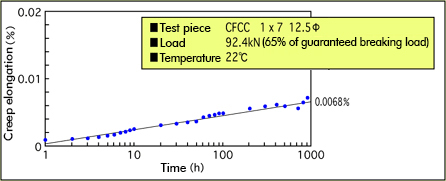
* CFCC 1x7 12.5mm dia.

High Tensile Fatigue Resistance

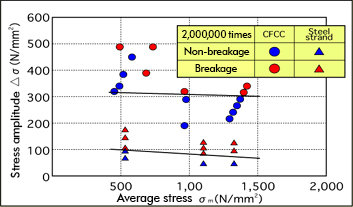
CFCC has higher tensile fatigue resistance in comparison with PC steel strands.

Low Relaxation

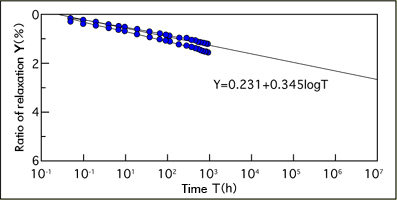
CFCC's relaxation ratio is on the same level as low relaxation PC steel strands.

Test specimen: CFCC 1x7 dia. 12.5mm, The initial load: 70% of guaranteed breaking load, The ambient temperature: 20°C±2°C)

Small Creep Elongation

CFCC's creep elongation is smaller than that of other FRP materials such as glass fibers or aramid fibers, and almost equal to steel cables.